算子融合fusion

1. 啥是fusion

fusion我们简单理解：

1. 在机器学习图优化中，图上一般是算子融合（看不到具体计算，高层次抽象），指明说这几个算子合并成类似一个kernel 进行计算。 💡
2. 在能看到loop（能看到具体计算的）的优化中，我们把两个loop 处理的内容，合并成一个loop进行处理。 🍉

MLIR中提供的算子fusion机制，并且经常使用的fusion处于linalg中，另外一部分在scf和affine 仿射变换中。

2. linalg fusion

当前2025-04-09，观察到linalg中提供的fusion分为两类：(社区的Mehash大佬负责实现和维护）🍉

1. generic op，且仅限于elementwise 类型op的fusion 。 💡
   1. 这种fusion实现比较简单。逻辑上分为这么几步完成的：
      1. 从当前generic的operand，查看operand的producer，是不是elementwise的op，比如必须要求producer的for loop都是parallel轴（有reduction的一定不是elementwise）。检查producer是不是pure tensor语义。
         1. 啥是pure tensor 语义呢？为啥需要标记是pure tensor语义呢？
         特性pure tensorpure memref‌数据抽象‌逻辑多维数组物理内存引用‌可变性‌不可变（操作生成新结果）可变（直接修改内存）‌副作用‌无可能有（如内存修改）‌优化阶段‌高层次算法优化低层次内存布局优化‌典型操作‌extract_slice, matmulsubview, load/store通过类型和操作语义的严格区分，MLIR能够在不同抽象层次上实现高效优化，同时保持代码可读性和可维护性‌。 🪫
      2. 如果producer检查通过，那么可以进行融合。融合就是比较暴力的思路，将producer op和当前的consumer op，operand, indexing_map, result 按照正确顺序统一放到一个新的operand, indexing_map, result中。处理好这些参数后，即可以将producer region内容和当前consumer op的region内容统一写到同一个region。
         1. 融合linalg region时比较麻烦，除了要处理block的argument，正确的yield内容，还要处理index operation，官方通过affine apply处理索引，消除对索引计算的干扰。
   2. tiling后的fusion。tiling指的是利用社区提供的TilingOpInterface 接口，对实现了这个Interface的op进行tiling。 💡
      1. TilingOpInterface 每个可以做tiling的op都应该继承这个接口。继承了这个接口的op就可以实现适合这个op的tiling 方法。用户去实现tiling pass 时，使用官方提供的这个方法：
         1. 
         2. 其中的SCFTilingOptions 包括了SCFTilingOptions &setTileSizes(ArrayRef<OpFoldResult> ts); 这个方法。用户可以指定op每个维度的tiling size，让这个方法帮你生成对应的tiling for loop。详细解析这个方法的实现不是我们这里的重点，重点在于linalg op的tiling的实现通过tensor.extract_slice和memref::subview以及tensor.insert_slice 这三个op 辅助实现tile逻辑。Tiling后的IR一般长下面这样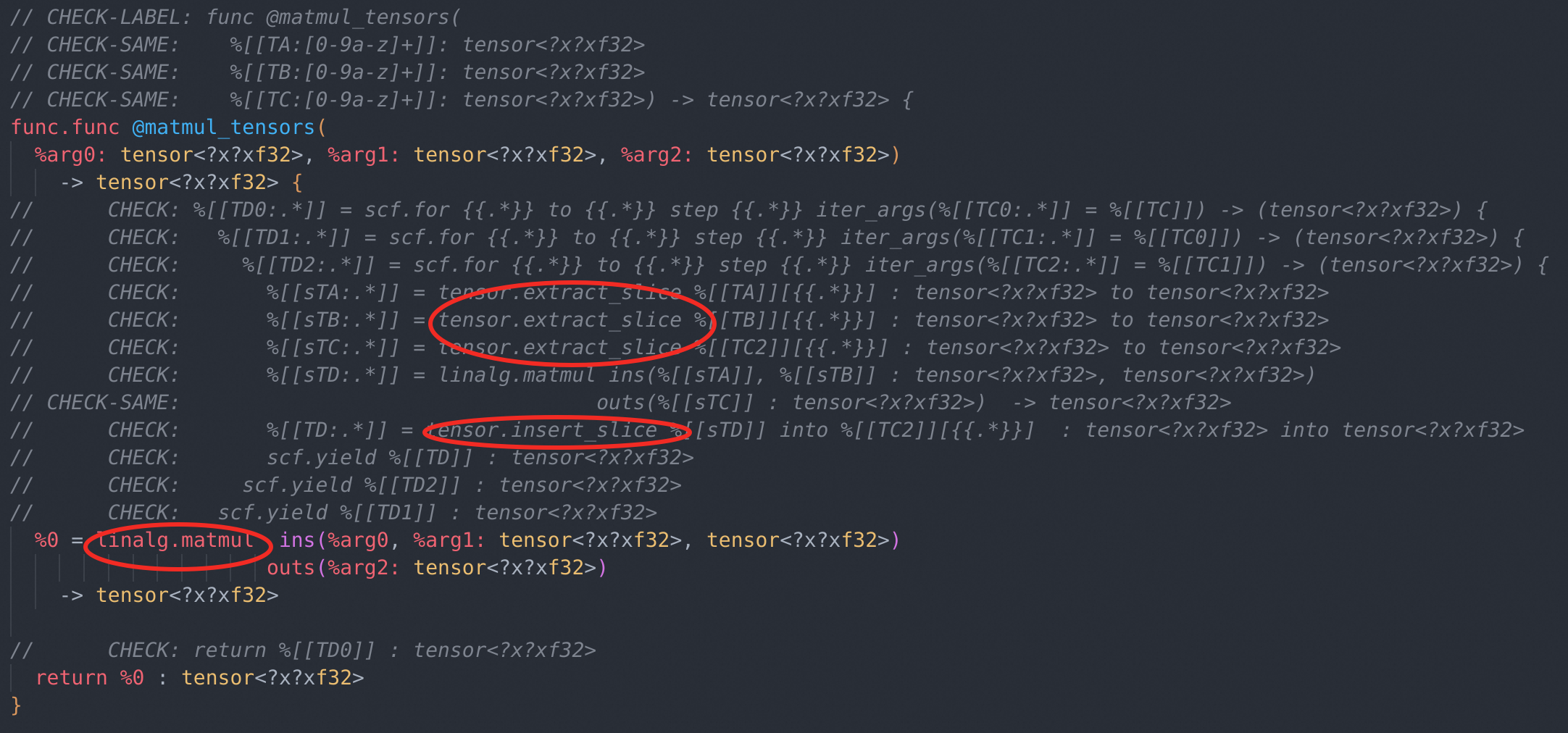：由图片可以看到，一个linalg.matmul分别对matmul的A B C三个tensor借助上面提到的op进行了tile。
         3. tile完成后，就可以使用官方提供的tileConsumerAndFuseProducersUsingSCF方法，这个方法贪心地去tileconsumer ，然后fuse 它的producer。实现的主要逻辑如下：
            1. 由于Tiling后的IR一定会有extract_slice，所以，首先寻找tiled consumer op的所有的extract_slice op然后寻找extract_slice op的所有untiled producer ,对找到的所有untiled producer进行fuse。
            2. fuse producer 时，IR的insert point 直接在consumer 的extract slice 位置，这样可以直接将producer写在consumer的for loop 里。通过cloned一个新的producer（pass中尽量不要原地修改op），计算cloned producer所需的operand，然后仍然使用extract_slice 对cloned producer进行与consumer相同的tiling，将完成的tiling结果replace原始的op，最后的IR即可完成两个op的fusion。
      2. 我们可以看到，社区提供的这些方法仍然不够成熟。第二种fusion的tilingandfusion虽然一定程度上可以完成multi-level for loop fusion，但是fuse 比较僵硬，僵硬的点在于：
         1. 只能由tiling的consumer去fuse producer。
         2. fuse producer的位置只能保持和consumer inner most loop的位置，不能灵活fuse合适的位置，没有一个合适的算法将producer放在consumer的multi-level loop中哪个level。当一个producer 有多个consumer时，可能需要将producer放在外层loop中让后续所有consume同时使用。
2. scf dialect 中提供了SCFParallelLoopFusion ，看这个fusion的名字就知道，通过标记for loop 的类型是parallel，可以放心将前后loop body内容合并，不会破坏数据依赖。同时提供fuseIndependentSiblingForLoops 、fuseIndependentSiblingForallLoops fuse前后没有数据依赖的loop，这两个loop是sibling loop，且一定要没有数据依赖，scf中的这个方法由用户分析没有数据依赖后才能使用，有点鸡肋。 😈
3. affine 中也有fusion 的pass。affine loop的fusion，提供了两种机制：
   1. producer and consumer. 🔔
      1. 这种方式是fuse n对loop，比如某对loop之间有数据依赖，第一个loop计算结果写入某个memref中，第二个loop会从这个memref中读取数据。这个pass会将这两个loop body的内容按照顺序放到一起，防止因为破坏数据依赖而改变计算结果。affine.for %arg2 = 0 to 10 {
         affine.store %cst, %0[%arg2] : memref<10xf32>
         affine.store %cst, %1[%arg2] : memref<10xf32>
         }
         affine.for %arg2 = 0 to 10 {
         %2 = affine.load %0[%arg2] : memref<10xf32>
         %3 = arith.addf %2, %2 : f32
         affine.store %3, %arg0[%arg2] : memref<10xf32>
         }
         affine.for %arg2 = 0 to 10 {
         %2 = affine.load %1[%arg2] : memref<10xf32>
         %3 = arith.mulf %2, %2 : f32
         affine.store %3, %arg1[%arg2] : memref<10xf32>
         }
         ======> fusion result
         affine.for %arg2 = 0 to 10 {
          # first loop
         affine.store %cst, %0[0] : memref<1xf32>
         affine.store %cst, %1[0] : memref<1xf32>
          # second loop
         %2 = affine.load %1[0] : memref<1xf32>
         %3 = arith.mulf %2, %2 : f32
         affine.store %3, %arg1[%arg2] : memref<10xf32>
          # third loop
         %4 = affine.load %0[0] : memref<1xf32>
         %5 = arith.addf %4, %4 : f32
         affine.store %5, %arg0[%arg2] : memref<10xf32>
         }
      2. sibling fusion. 🏮
         1. 这种fusion前后loop没有数据依赖。但是计算的内容是需要从同一个memref中读取数据。
         
         affine.for %arg5 = 0 to 3 {
         affine.for %arg6 = 0 to 3 {
           %0 = affine.load %arg0[%arg5, %arg6] : memref<10x10xf32>
           %1 = affine.load %arg1[%arg5, %arg6] : memref<10x10xf32>
           %2 = arith.mulf %0, %1 : f32
           affine.store %2, %arg3[%arg5, %arg6] : memref<10x10xf32>
         }
         }
         affine.for %arg5 = 0 to 3 {
         affine.for %arg6 = 0 to 3 {
           %0 = affine.load %arg0[%arg5, %arg6] : memref<10x10xf32>
           %1 = affine.load %arg2[%arg5, %arg6] : memref<10x10xf32>
           %2 = arith.addf %0, %1 : f32
           affine.store %2, %arg4[%arg5, %arg6] : memref<10x10xf32>
         }
         }
         ======> fusion result:
         affine.for %arg5 = 0 to 3 {
         affine.for %arg6 = 0 to 3 {
         # first loop body
         %0 = affine.load %arg0[%arg5, %arg6] : memref<10x10xf32>
         %1 = affine.load %arg1[%arg5, %arg6] : memref<10x10xf32>
         %2 = arith.mulf %0, %1 : f32
         affine.store %2, %arg3[%arg5, %arg6] : memref<10x10xf32>
          # second loop body
         %3 = affine.load %arg0[%arg5, %arg6] : memref<10x10xf32>
         %4 = affine.load %arg2[%arg5, %arg6] : memref<10x10xf32>
         %5 = arith.addf %3, %4 : f32
         affine.store %5, %arg4[%arg5, %arg6] : memref<10x10xf32>
         }
         }
   fusion带来的好处显而易见，可以通过优化融合后的loop body，减少了冗余load store（内存操作），同时一个数据能计算多次，更加充分利用数据局部性。 🤑但是越复杂的场景，需要我们设计复杂的算法和cost model去计算和衡量，当前的两个loop是否能融合，融合后的性能是否好?cost model的设计也是复杂的考量，极端情况下，如果没有cost model，对任意能fuse的loop 进行fusion，一个loop中计算太多内容： 🫥
   1. 会有很多var spill到内存。cpu通用寄存器就那么几个，一个loop中临时变量太多，会spill。
   2. loop中的需要取的数据大于cpu缓存大小（一般cpu上我们考虑二级缓存即可，复杂case例外）。miss cache rate 增加，造成实际性能反而下降，这种情况我们宁可不fuse。
   它的实现原理，主要通过DependenceGraph 实现，具体的原理作者这里先留个未来再续。。。 🤣