target:
- analysis floating point。
- floating point accuracy and precision issue。
IEEE 754 floating-point
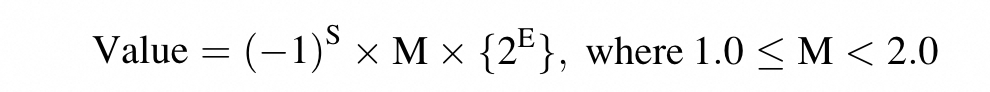
Some point:
- Sign(S) exponent(E) mantissa(M)
S=0positive number.S=1negative number.
2.1 Normalized Representation of M
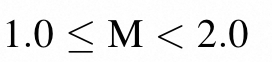
M makes the mantissa value for each floating-point number unique.
For example: 0.5
legal representation: 1x2^-1
other representation must cast to legal: 0.5 x 2^0
2.2 Excess Encoding of E
Determine the range of number that can be represented.
For example: E = 64
floating-point number being represented between 2^64and 2^65.
Negative number is 2^-64and 2^-63.
2^(n-1)is added to the two's complement representation. Two complement representation is a system where the negative value of a number can be derived by first complementing every bit of the value and adding 1 to the result.
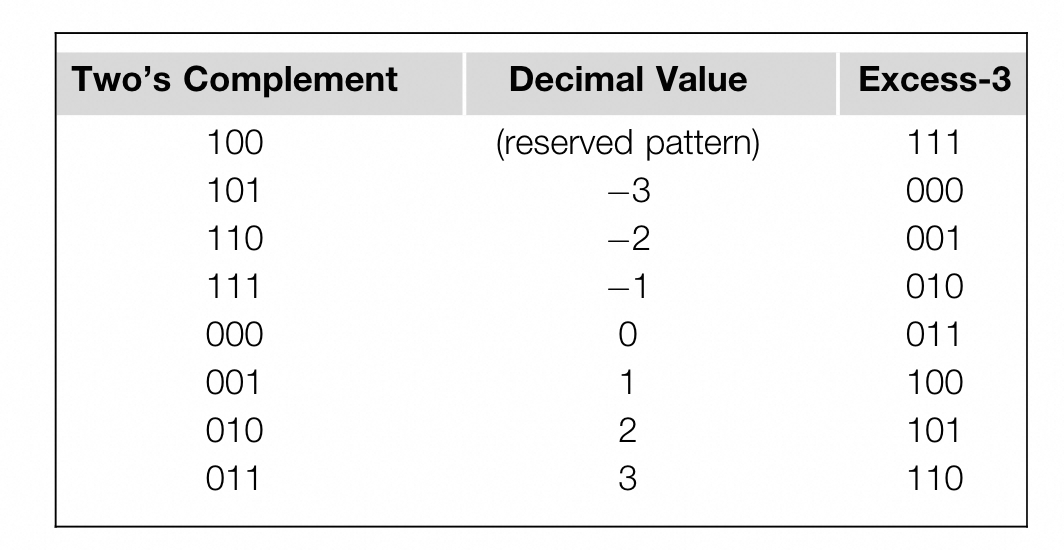
The advantage of excess representation:
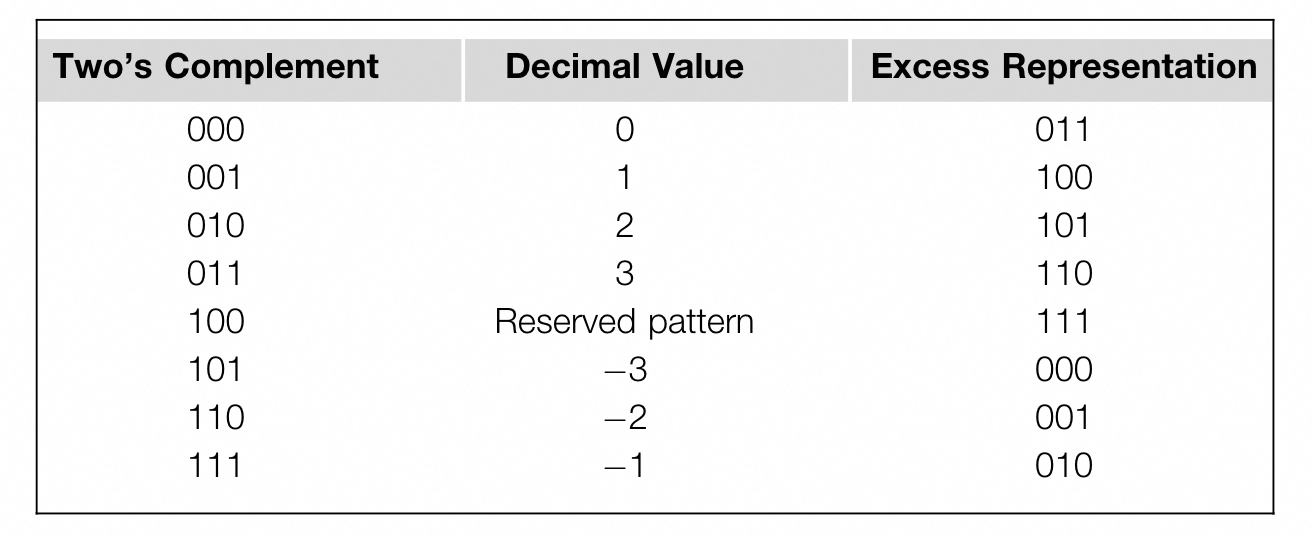
We can view all the number as unsigned number. We can see the picture ,we can compare the number directly use complement unsigned number. This is a desirable property for hardware implentation, because unsigned comparators are smaller and faster than signed comparators.
Another reason is:
I recommend an article for everyone who want to know why computer science use complement.
https://www.zhihu.com/question/20159860/answer/71256667

2.3 Observation
- Exponent bits define the major intervals of representable number.
- Mantissa bits define the number of representable numbers in each interval. If a value to be represented falls within one of the intervals, it will be rounded to one of these representable numbers.

Representable numbers become closer to each other toward the neighborhood of 0. For example, if we have $1 billion in bank, we may not notice $1 rounding error. But if we have $10, $1 rounding error would be much more noticeable!
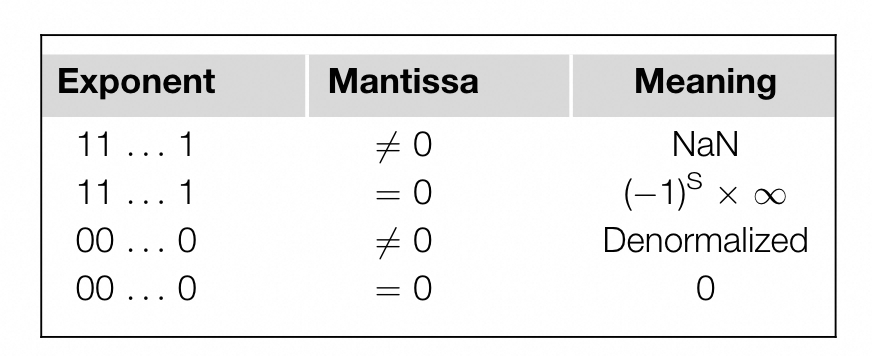
Special pattern.
2.4 rounding
When the result cannot be exactly represented and hus required rouding. Rounding occurs if the mantissa of the result value needs too many bits to be represented exactly.
Assume that we have a 5-bit representation.
add: 1.00 * 2^-2 (0,00,01)to 1.00 * 2^1(0,10,00)
step:
- different M: smaller mantissa of one with smaller exponent value must be right shifted util the exponents are equal before being added to the larger mantissa value.
- The addition becomes:
1.0x2^1+0.001x2^1, the ideal result would be1.001 x 2^1. The result require 3 bit mantissa, the best one can do is generate the closest representable number, which is1.01 x 2^1. This will introduce a error0.001 x 2^1,which is half the place value of the least significant place.
- The addition becomes:
2.5 algorithnm considerations
Numerical algorithm often must sum up a large number of values. For exmaple, the dot product in matrix multiplication needs to sum up pairwise products of input matrix elements.
Ideally, the order of summing these values should not affect the final total. However, the order of summing these values can affect the accuracy of the final result such as we need to performa a sum reduction on 4 numbers in 5-bit representation:
1.00 x 2^0+ 1.00 x 2^0+ 1.00 x 2^-2+ 1.00x2^-2
If we add up the number in strict sequencial order:
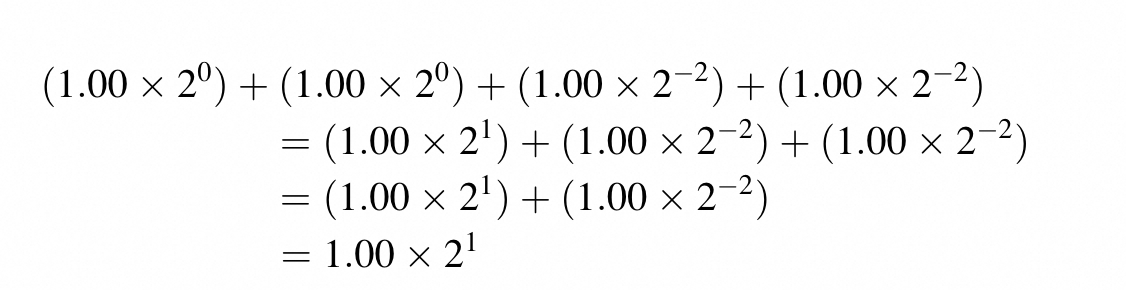
Note that in the second step and third step the smaller operands simply disapper because they are too small compare to the larger operands.
Another add order:
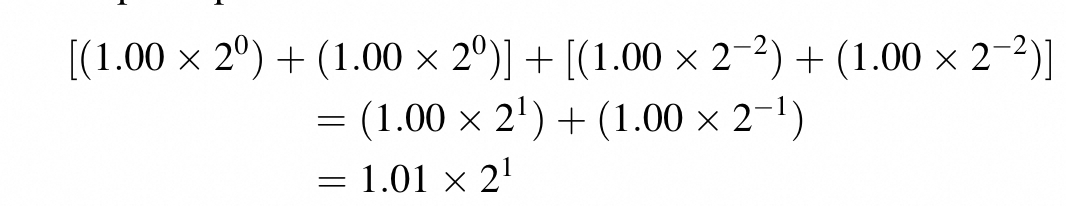
The results are different from the two results.
This discrepancy often surprise application developers who are not familiar with floating-point precision and accuracy considerations.
A common technique to maximize floating-point arithmetic accuracy is to presort data before a reduction computation. If we presort the data according to ascending numerical order:
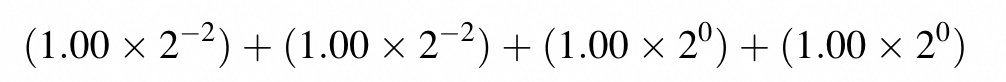
When we do sumup , it guaranteed that numbers with numerical values close to each other are in the same group. Therefore, when we perform addition in these groups, we will likely have accurate results.
This is an important reason why sorting is frequently used in massively parallel numerical algorithm.

Comments 1 条评论